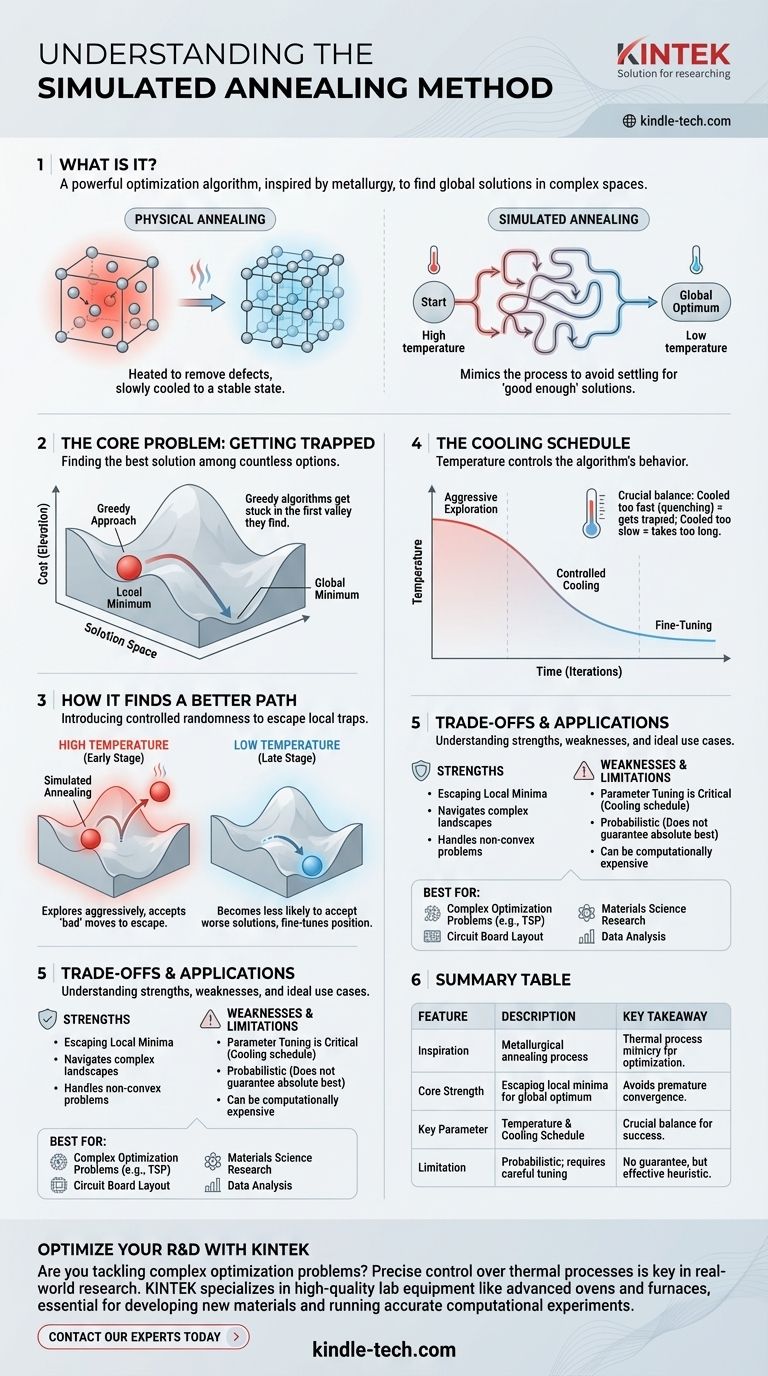
Kurz gesagt, Simulated Annealing (simuliertes Glühen) ist ein mächtiger Optimierungsalgorithmus, der verwendet wird, um eine gute (und oft globale) Lösung in einem riesigen und komplexen Suchraum zu finden. Er ist direkt inspiriert vom metallurgischen Glühprozess, bei dem ein Material erhitzt und dann langsam abgekühlt wird, um Defekte zu beseitigen und einen stabilen, energiearmen kristallinen Zustand zu erreichen. Der Algorithmus ahmt diesen physikalischen Prozess nach, um abstrakte rechnerische Probleme zu lösen.
Im Kern vermeidet Simulated Annealing die häufige Falle, sich mit einer "gut genug" Lösung zufrieden zu geben, indem es den physikalischen Prozess des Metallglühens nachahmt. Es beginnt mit der Erkundung einer breiten Palette von Möglichkeiten (hohe Temperatur) und verengt seinen Fokus allmählich auf eine hochwertige, stabile Lösung (niedrige Temperatur).
Das Kernproblem: Gefangen sein
Um Simulated Annealing zu verstehen, müssen Sie zunächst das Problem verstehen, das es löst: die bestmögliche Lösung unter unzähligen Optionen zu finden, eine Aufgabe, die als Optimierung bekannt ist.
Die Landschaft der Lösungen
Stellen Sie sich vor, jede mögliche Lösung Ihres Problems ist ein Punkt auf einer riesigen, hügeligen Landschaft. Die Höhe jedes Punktes stellt seine "Kosten" dar – je niedriger die Höhe, desto besser die Lösung. Ihr Ziel ist es, den tiefsten Punkt auf der gesamten Karte zu finden, das globale Minimum.
Der "gierige" Ansatz und sein Fehler
Ein einfacher Algorithmus, oft als Hill-Climbing bezeichnet, würde an einem zufälligen Punkt beginnen und sich immer bergab bewegen. Dies ist ein "gieriger" Ansatz, da er nur Bewegungen akzeptiert, die eine sofortige Verbesserung ergeben.
Das Problem ist, dass diese Methode im ersten Tal stecken bleibt, das sie findet – einem lokalen Minimum. Sie hat keine Möglichkeit zu wissen, ob ein viel tieferes Tal, das globale Minimum, gleich hinter dem nächsten Hügel existiert.
Wie Simulated Annealing einen besseren Weg findet
Simulated Annealing überwindet diese Einschränkung, indem es ein kontrolliertes Zufallselement einführt, das es ihm ermöglicht, diesen lokalen Fallen zu entkommen.
Die Inspiration: Physikalisches Glühen
In der Metallurgie gibt das Erhitzen eines Metalls seinen Atomen genügend Energie, um sich frei zu bewegen und aus suboptimalen, defekten Strukturen auszubrechen. Wenn das Metall langsam abgekühlt wird, haben die Atome Zeit, sich in einem hochgeordneten, starken Kristallgitter – einem Zustand minimaler Energie – anzuordnen.
Der Algorithmus: Temperatur als Steuerknopf
Simulated Annealing übernimmt dieses Konzept, indem es einen Temperaturparameter einführt. Dies ist keine physikalische Temperatur, sondern eine Variable, die das Verhalten des Algorithmus steuert.
Der Algorithmus beginnt mit einer hohen Temperatur. In diesem Zustand erkundet er die Lösungslandschaft aggressiv, ähnlich den energetischen Atomen in heißem Metall. Er hat eine hohe Wahrscheinlichkeit, Bewegungen zu akzeptieren, die schlechter sind als seine aktuelle Position. Dies ist der Schlüssel: Eine "schlechte" Bewegung zu machen, ermöglicht es ihm, aus einem lokalen Minimum herauszuklettern.
Der Abkühlplan
Während der Algorithmus läuft, wird die Temperatur gemäß einem Abkühlplan schrittweise gesenkt. Wenn die Temperatur sinkt, wird der Algorithmus immer unwahrscheinlicher, eine schlechtere Lösung zu akzeptieren.
Am Ende, bei einer sehr niedrigen Temperatur, verhält sich der Algorithmus wie die einfache Hill-Climbing-Methode, akzeptiert nur Verbesserungen und verfeinert seine Position in dem hoffentlich globalen Minimum.
Die Kompromisse verstehen
Wie jedes mächtige Werkzeug ist Simulated Annealing keine Universallösung. Das Verständnis seiner Einschränkungen ist entscheidend für seinen effektiven Einsatz.
Stärke: Entkommen aus lokalen Minima
Sein Hauptvorteil ist seine Fähigkeit, komplexe, nicht-konvexe Landschaften mit vielen lokalen Minima zu navigieren. Für Probleme, bei denen gierige Algorithmen konsequent versagen, ist Simulated Annealing eine ausgezeichnete Wahl.
Schwäche: Parameterabstimmung ist entscheidend
Die Leistung des Algorithmus ist stark abhängig vom Abkühlplan. Wenn zu schnell abgekühlt wird, kann er trotzdem in einem lokalen Minimum gefangen werden ("Quenching"). Wenn zu langsam abgekühlt wird, kann es eine unpraktische Zeit dauern, eine Lösung zu finden. Den richtigen Plan zu finden, erfordert oft Experimente.
Einschränkung: Es ist eine probabilistische Methode
Simulated Annealing garantiert nicht, dass es die absolut beste Lösung (das globale Minimum) findet. Es ist eine Heuristik, was bedeutet, dass es darauf ausgelegt ist, eine sehr gute Lösung in einer angemessenen Zeit zu finden. Es besteht immer eine statistische Chance, dass es in einem suboptimalen Zustand landet.
Die richtige Wahl für Ihr Problem treffen
Nutzen Sie diese Anleitung, um zu entscheiden, ob Simulated Annealing der richtige Ansatz für Ihre Optimierungsaufgabe ist.
- Wenn Ihr Hauptaugenmerk darauf liegt, ein komplexes Problem mit vielen Fallen (lokalen Minima) zu lösen: Simulated Annealing ist eines der besten Werkzeuge für diese Aufgabe, insbesondere für klassische Probleme wie das Problem des Handlungsreisenden oder das Layout von Leiterplatten.
- Wenn Ihr Hauptaugenmerk darauf liegt, eine nachweislich optimale Lösung mit maximaler Geschwindigkeit zu finden: Sie sollten zuerst prüfen, ob Ihr Problem einfach genug ist (z. B. konvex), um von einem schnelleren, deterministischen Algorithmus wie der linearen Programmierung oder einem standardmäßigen gierigen Ansatz gelöst zu werden.
Letztendlich bietet Simulated Annealing einen robusten Rahmen, um riesige und schwierige Suchräume zu navigieren, um hochwertige Lösungen zu finden, wo einfachere Methoden versagen.
Zusammenfassungstabelle:
| Merkmal | Beschreibung |
|---|---|
| Inspiration | Metallurgischer Glühprozess (Erhitzen & langsames Abkühlen) |
| Kernstärke | Entkommen aus lokalen Minima, um ein globales Optimum zu finden |
| Schlüsselparameter | Temperatur & Abkühlplan |
| Am besten geeignet für | Komplexe Optimierungsprobleme mit vielen lokalen Fallen |
| Einschränkung | Probabilistisch; erfordert sorgfältige Parameterabstimmung |
Optimieren Sie Ihre Forschung und Entwicklung mit KINTEK
Stehen Sie vor komplexen Optimierungsproblemen in der Materialwissenschaft, der Chemieingenieurwissenschaft oder der Datenanalyse? Die Prinzipien des simulierten Glühens sind von realen thermischen Prozessen inspiriert, und eine präzise Kontrolle dieser Prozesse in Ihrem Labor ist entscheidend.
KINTEK ist spezialisiert auf hochwertige Laborgeräte, einschließlich fortschrittlicher Öfen und Herde, die die gleichmäßige Erwärmung und kontrollierte Abkühlung bieten, die für Forschung und Entwicklung unerlässlich sind. Ob Sie neue Materialien entwickeln oder rechnerische Experimente durchführen, zuverlässige Geräte sind die Grundlage für genaue Ergebnisse.
Kontaktieren Sie noch heute unsere Experten, um die perfekte Laborlösung zur Verbesserung Ihrer Optimierungsworkflows und zur Erzielung bahnbrechender Ergebnisse zu finden.
Ähnliche Produkte
- Ofen mit Wasserstoffatmosphäre
- Kleiner Vakuum-Wolframdraht-Sinterofen
- Maschenbandofen mit kontrollierter Atmosphäre
- 1400℃ Ofen mit kontrollierter Atmosphäre
- Ziehdüse mit Nano-Diamantbeschichtung, HFCVD-Ausrüstung
Andere fragen auch
- Was ist Ofenatmosphäre? Ein Leitfaden für kontrolliertes Erhitzen für überlegene Ergebnisse
- Was ist der Nutzen eines Schutzgasofens? Präzise, kontaminationsfreie Wärmebehandlung erreichen
- Was ist das häufigste Edelgas in der Atmosphäre? Entdecken Sie die Rolle von Argon
- Welche Sicherheitsvorkehrungen sollten Sie beim Arbeiten mit einer Wärmequelle treffen? Wesentliche Richtlinien für eine sichere Laborumgebung
- Was ist der Unterschied zwischen modifizierter Atmosphäre und kontrollierter Atmosphäre? Lebensmittelkonservierungsmethoden meistern
