Wie beeinflusst die Stichprobengröße die erforderliche Messgenauigkeit? Optimieren Sie Ihre Datenqualität

Kurz gesagt, eine größere Stichprobengröße ändert nichts an der inhärenten Genauigkeit Ihres Messinstruments, erhöht aber die Genauigkeit der Schlussfolgerungen, die Sie aus Ihren Daten ziehen können, dramatisch. Durch das Sammeln weiterer Proben reduzieren Sie den „Stichprobenfehler“, der die Unsicherheit darstellt, die sich aus der Beobachtung eines Teils einer Gruppe anstelle des Ganzen ergibt. Dies bedeutet, dass Ihre Ergebnisse mit größerer Wahrscheinlichkeit eine wahre Darstellung der gesamten Population sind.

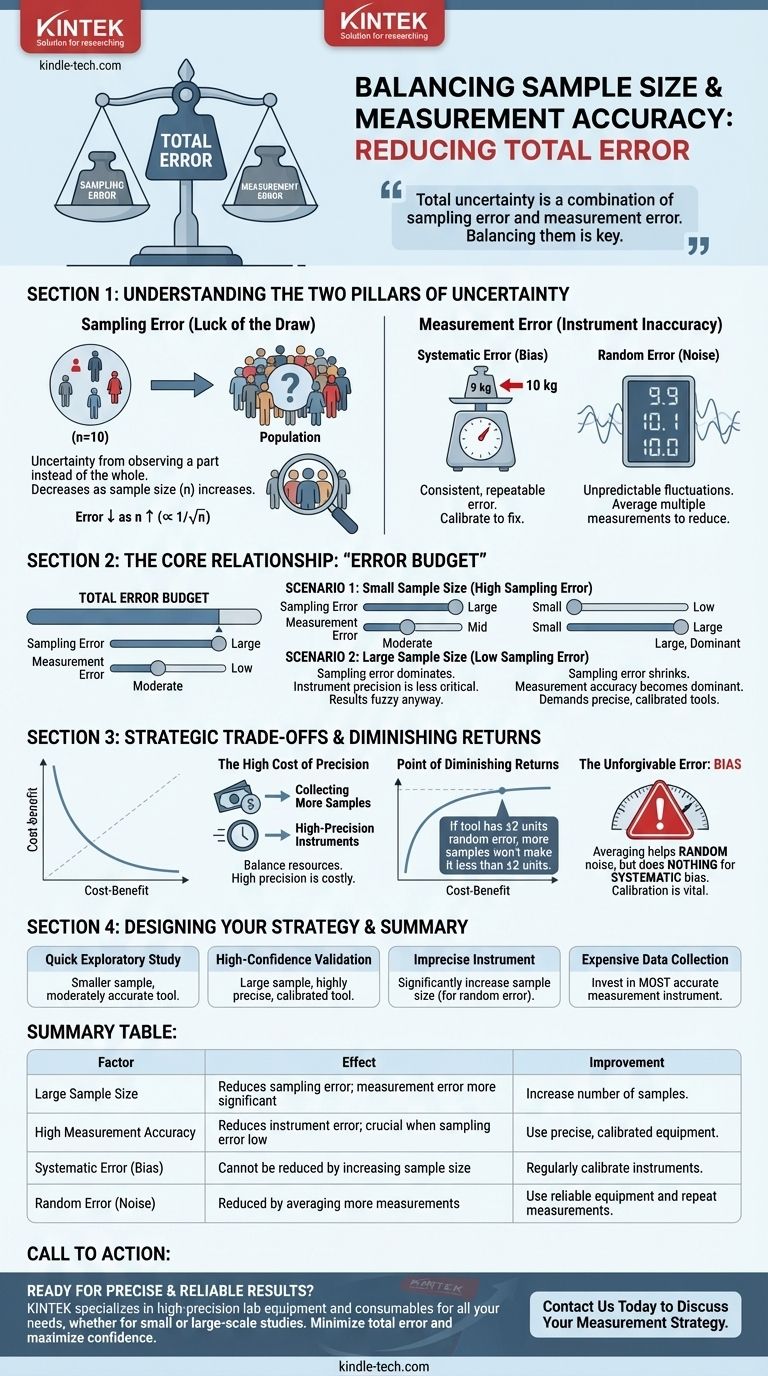
Das Kernproblem ist nicht nur die Stichprobengröße; es geht darum, zwei verschiedene Fehlerquellen auszugleichen. Ihre Gesamtunsicherheit ist eine Kombination aus Stichprobenfehler (aus der Größe Ihrer Stichprobe) und Messfehler (aus der Qualität Ihres Werkzeugs). Das Verständnis, wie diese beiden interagieren, ist der Schlüssel zur Gestaltung einer effektiven Studie.

Die zwei Säulen der Unsicherheit: Stichproben- vs. Messfehler

Um die Beziehung vollständig zu erfassen, müssen Sie zwischen den beiden grundlegenden Fehlertypen unterscheiden, die Ihre Ergebnisse beeinflussen können. Sie sind nicht austauschbar.

Stichprobenfehler verstehen

Der Stichprobenfehler ist das „Glück des Zufalls“. Es ist der zufällige Unterschied zwischen den Merkmalen Ihrer Stichprobe und den Merkmalen der gesamten Population, die sie repräsentieren soll.

Stellen Sie sich vor, Sie versuchen, die Durchschnittsgröße aller Menschen in einer Stadt zu bestimmen, indem Sie nur 10 Personen messen. Sie könnten versehentlich eine ungewöhnlich große oder kleine Gruppe auswählen.

Dieser Fehler ist kein Irrtum; er ist eine statistische Realität. Die gute Nachricht ist, dass er vorhersagbar und kontrollierbar ist. Wenn Ihre Stichprobengröße (n) zunimmt, verringert sich Ihr Stichprobenfehler proportional zur Quadratwurzel der Stichprobengröße (1/√n). Eine größere Stichprobe spiegelt die wahre Population mit größerer Wahrscheinlichkeit wider.

Messfehler verstehen

Der Messfehler ist die Ungenauigkeit, die Ihrem Messgerät oder Ihrer Methode inhärent ist. Er hat nichts damit zu tun, wie viele Proben Sie nehmen.

Dieser Fehler tritt in zwei Formen auf:

1. Systematischer Fehler (Bias): Ein konsistenter, wiederholbarer Fehler. Denken Sie an eine Waage, die immer 1 kg zu viel anzeigt. Mehr Messungen werden dies nicht beheben; Sie erhalten lediglich ein sehr präzises, aber falsches Ergebnis.
2. Zufälliger Fehler (Rauschen): Unvorhersehbare Schwankungen bei der Messung. Denken Sie an eine digitale Waage, deren letzte Ziffer leicht flackert.

Das Mitteln vieler Messungen kann dazu beitragen, den Effekt des zufälligen Fehlers zu reduzieren, aber es kann systematische Fehler niemals korrigieren. Die Genauigkeit Ihres Werkzeugs setzt eine harte Grenze für die letztendliche Wahrhaftigkeit Ihrer Daten.

Wie Stichprobengröße und Messgenauigkeit interagieren

Die entscheidende Erkenntnis ist, dass diese beiden Fehler zu Ihrem gesamten „Fehlerbudget“ beitragen. Ihr Ziel ist es, den Gesamtfehler zu minimieren, und wie Sie Ressourcen zur Bekämpfung jedes Fehlertyps zuweisen, hängt von Ihrer Situation ab.

Die Kernbeziehung: Ihr „Fehlerbudget“

Stellen Sie sich Ihr gewünschtes Konfidenzniveau als Budget für den Gesamtfehler vor. Sie „geben“ dieses Budget für eine Kombination aus Stichprobenfehler und Messfehler aus.

Wenn eine Fehlerquelle sehr groß ist, wird sie Ihre Ergebnisse dominieren, und die Reduzierung der anderen Quelle kann wenig praktische Wirkung haben.

Szenario 1: Kleine Stichprobengröße

Wenn Ihre Stichprobengröße klein ist, ist der Stichprobenfehler hoch. Er ist fast immer der größte Beitrag zu Ihrer Gesamtunsicherheit.

In dieser Situation ist die Präzision Ihres Messgeräts weniger kritisch. Ihr Ergebnis wird ohnehin aufgrund des „Glücks des Zufalls“ bei der Stichprobenziehung unscharf sein, sodass ein kleiner Messfehler das Gesamtbild nicht wesentlich verschlechtert.

Szenario 2: Große Stichprobengröße

Wenn Sie Ihre Stichprobengröße erhöhen, schrumpft der Stichprobenfehler dramatisch. Ihr Stichprobenmittelwert nähert sich immer mehr dem wahren Populationsmittelwert an.

Hier wird die Frage des Benutzers besonders aufschlussreich. Eine große Stichprobengröße erhöht effektiv die Anforderung an genaue Messungen. Wenn der Stichprobenfehler verschwindet, wird jeder Fehler Ihres Instruments zur dominanten Unsicherheitsquelle.

Wenn Ihr Messgerät einen systematischen Bias aufweist, liefert eine riesige Stichprobengröße nur eine sehr präzise Schätzung des falschen Wertes. Dies verstärkt die Bedeutung eines gut kalibrierten und genauen Instruments.

Die Kompromisse verstehen

Die Entscheidung über Stichprobengröße und Instrumentenqualität ist ein strategischer Balanceakt, der oft von Zeit und Geld bestimmt wird.

Die hohen Kosten der Präzision

Das Sammeln weiterer Proben kostet Zeit und Ressourcen. Ebenso sind hochpräzise, perfekt kalibrierte Instrumente teuer. Sie müssen entscheiden, wo Sie investieren möchten.

Geld in eine massive Stichprobengröße zu stecken, ist verschwenderisch, wenn Ihre Ergebnisse letztendlich durch ein billiges, ungenaues Messgerät begrenzt werden.

Der Punkt des abnehmenden Ertrags

Es gibt einen Punkt, an dem eine Erhöhung der Stichprobengröße fast keinen Nutzen mehr bringt. Wenn Ihr Messgerät einen inhärenten Zufallsfehler von ±2 Einheiten aufweist, können Sie niemals ein kleineres Konfidenzintervall erreichen, egal wie viele Proben Sie nehmen.

Ähnlich ist der Kauf eines Millionen-Dollar-Instruments sinnlos, wenn Sie nur drei Proben nehmen wollen, da Ihr massiver Stichprobenfehler die unglaubliche Präzision des Instruments in den Schatten stellen wird.

Der unverzeihliche Fehler: Bias

Denken Sie daran, dass eine Erhöhung der Stichprobengröße dazu beiträgt, zufälliges Rauschen auszugleichen, aber absolut nichts dazu beiträgt, systematischen Bias zu beheben.

Die Kalibrierung Ihrer Instrumente zur Eliminierung systematischer Fehler ist oft der wichtigste Schritt, den Sie unternehmen können, um die Integrität Ihrer Daten zu gewährleisten, unabhängig von der Stichprobengröße.

Ihre Messstrategie gestalten

Es gibt keine einzelne „richtige“ Stichprobengröße oder Genauigkeitsstufe. Die richtige Wahl hängt vollständig von Ihrem Ziel und Ihren Einschränkungen ab.

• Wenn Ihr Hauptaugenmerk auf einer schnellen explorativen Studie liegt: Eine kleinere Stichprobengröße in Kombination mit einem mäßig genauen Instrument kann ausreichen, um wichtige Trends zu identifizieren und zukünftige Forschung zu leiten.
• Wenn Ihr Hauptaugenmerk auf einer hochkonfidenten Validierung liegt (z. B. behördliche Genehmigung): Sie benötigen sowohl eine große, sorgfältig ausgewählte Stichprobe als auch ein hochpräzises, kalibriertes Instrument, um sowohl Stichproben- als auch Messfehler in einem überprüfbaren Maße zu minimieren.
• Wenn Ihr Messinstrument als ungenau bekannt ist: Sie können dies durch eine signifikante Erhöhung Ihrer Stichprobengröße kompensieren, aber nur, wenn der Fehler zufällig und nicht systematisch ist. Dies reduziert Ihre Gesamtunsicherheit, aber nur bis zu der Grenze, die durch die Mängel des Instruments gesetzt wird.
• Wenn das Sammeln von Proben extrem teuer oder schwierig ist (z. B. Weltraumforschung): Sie müssen in das genaueste Messinstrument investieren, das möglich ist, um den maximalen Wert aus jedem kostbaren Datenpunkt zu ziehen.

Letztendlich geht es beim Ausbalancieren von Stichprobengröße und Messgenauigkeit darum, Ihre Ressourcen strategisch zu verteilen, um die bedeutendsten Unsicherheitsquellen in Ihrem spezifischen Kontext zu bekämpfen.

Zusammenfassungstabelle:

Faktor	Auswirkung auf die Ergebnisse	Wie zu verbessern
Große Stichprobengröße	Reduziert den Stichprobenfehler; macht den Messfehler signifikanter.	Erhöhen Sie die Anzahl der gemessenen Proben.
Hohe Messgenauigkeit	Reduziert den Instrumentenfehler; entscheidend, wenn der Stichprobenfehler gering ist.	Verwenden Sie präzise, gut kalibrierte Geräte.
Systematischer Fehler (Bias)	Kann nicht durch Erhöhung der Stichprobengröße reduziert werden.	Regelmäßige Kalibrierung der Instrumente.
Zufälliger Fehler (Rauschen)	Kann durch Mittelung mehrerer Messungen reduziert werden.	Verwenden Sie zuverlässige Geräte und wiederholen Sie Messungen.

Bereit für präzise und zuverlässige Ergebnisse in Ihrem Labor?

Das richtige Gleichgewicht zwischen Stichprobengröße und Messgenauigkeit ist entscheidend für die Integrität Ihrer Daten. KINTEK ist spezialisiert auf hochpräzise Laborgeräte und Verbrauchsmaterialien und deckt alle Ihre Laborbedürfnisse ab. Ob Sie Instrumente mit überragender Genauigkeit für kleine Stichprobenmengen oder robuste Geräte für groß angelegte Studien benötigen, wir haben die Lösung, um Ihren Gesamtfehler zu minimieren und das Vertrauen in Ihre Ergebnisse zu maximieren.

Kontaktieren Sie uns noch heute, um zu besprechen, wie unsere Produkte Ihre Messstrategie verbessern können. Lassen Sie sich von unseren Experten bei der Auswahl der perfekten Werkzeuge für Ihre spezifische Anwendung unterstützen.

#Kontaktformular