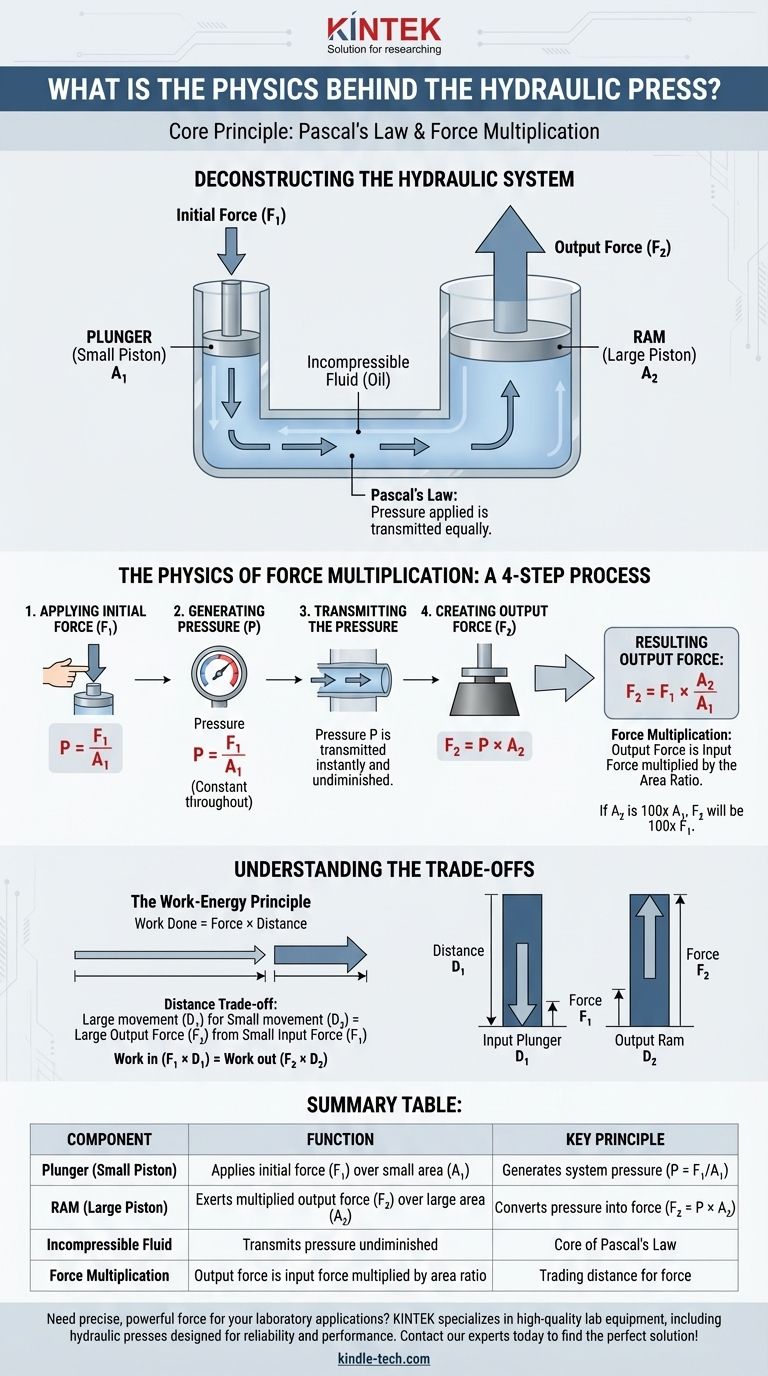
Das Kernprinzip einer hydraulischen Presse ist das Pascalsche Gesetz, das eine immense Kraftverstärkung mithilfe einer inkompressiblen Flüssigkeit ermöglicht. Dieses Gesetz besagt, dass jeder Druck, der auf eine Flüssigkeit in einem geschlossenen System ausgeübt wird, sich gleichmäßig in der gesamten Flüssigkeit ausbreitet. Eine hydraulische Presse nutzt dies aus, indem sie eine kleine Anfangskraft auf eine kleine Fläche anwendet, um eine viel größere Ausgangskraft über eine größere Fläche zu erzeugen.
Die grundlegende Erkenntnis ist, dass eine hydraulische Presse keine Energie erzeugt, sondern vielmehr die Kraft vervielfacht. Dies erreicht sie, indem sie eine kleine Kraft, die auf einen kleinen Kolben ausgeübt wird, in einen systemweiten Druck umwandelt, der dann auf einen größeren Kolben wirkt, um eine proportional größere Ausgangskraft zu erzeugen.
Den hydraulischen Aufbau zerlegen
Um die Physik zu verstehen, müssen wir uns zunächst die wesentlichen Komponenten ansehen, aus denen jede hydraulische Presse besteht. Diese Teile arbeiten in einem geschlossenen System zusammen, um Kraft zu übertragen und zu vervielfachen.
Die zwei Kolben: Stößel und Arbeitskolben
Fast jede hydraulische Presse hat zwei Kolben unterschiedlicher Größe. Der kleinere Kolben, oft als Stößel bezeichnet, ist der Ort, an dem die anfängliche, kleinere Kraft angewendet wird. Der größere Kolben, bekannt als Arbeitskolben, übt die massive Druckkraft aus, um die Arbeit zu verrichten.
Die inkompressible Flüssigkeit
Die Kolben sind in Zylindern untergebracht, die durch einen Kanal verbunden sind, der mit einer inkompressiblen Flüssigkeit, typischerweise einem speziellen Öl, gefüllt ist. "Inkompressibel" ist die Schlüsseleigenschaft – es bedeutet, dass sich das Volumen der Flüssigkeit unter Druck nicht ändert. Dies stellt sicher, dass, wenn Sie die Flüssigkeit an einem Ende drücken, sie diese Kraft sofort und ohne "zusammengedrückt" zu werden an das andere Ende überträgt.
Die Physik der Kraftverstärkung
Die wahre Genialität der hydraulischen Presse liegt darin, wie sie die Beziehung zwischen Kraft, Druck und Fläche nutzt. Der Prozess ist eine klare, vierstufige Anwendung des Pascalschen Gesetzes.
Schritt 1: Anwenden der Anfangskraft (F₁)
Der Prozess beginnt, wenn eine relativ kleine Kraft (F₁) auf den kleinen Eingangskolben, den Stößel, ausgeübt wird. Dieser Kolben hat eine kleine Oberfläche (A₁).
Schritt 2: Druck erzeugen (P)
Diese Anfangskraft erzeugt Druck in der Hydraulikflüssigkeit. Die Höhe des Drucks wird durch die Formel Druck = Kraft / Fläche definiert. Der Druck (P) im System wird also berechnet als P = F₁ / A₁.
Schritt 3: Druck übertragen
Hier ist das Pascalsche Gesetz entscheidend. Das Gesetz garantiert, dass der soeben erzeugte Druck (P) sofort und unvermindert auf jeden Teil der eingeschlossenen Flüssigkeit übertragen wird. Der auf den großen Arbeitskolben wirkende Druck ist genau derselbe wie der Druck unter dem kleinen Stößel.
Schritt 4: Erzeugen der Ausgangskraft (F₂)
Dieser konstante Druck (P) drückt nun gegen den großen Ausgangskolben, den Arbeitskolben, der eine viel größere Oberfläche (A₂) hat. Die resultierende Ausgangskraft (F₂) wird durch Umstellen der Druckformel berechnet: Kraft = Druck × Fläche.
Daher ist die Ausgangskraft F₂ = P × A₂.
Da wir wissen, dass P = F₁ / A₁, können wir dies in die zweite Gleichung einsetzen, um die direkte Beziehung zu sehen: F₂ = (F₁ / A₁) × A₂. Dies kann vereinfacht werden, um zu zeigen, dass die Ausgangskraft die Eingangskraft multipliziert mit dem Verhältnis der Flächen ist: F₂ = F₁ × (A₂ / A₁).
Wenn die Fläche des Arbeitskolbens (A₂) 100-mal größer ist als die Fläche des Stößels (A₁), ist die Ausgangskraft (F₂) 100-mal größer als die Eingangskraft (F₁).
Die Kompromisse verstehen
Diese Kraftverstärkung verstößt nicht gegen die Gesetze der Physik und ist keine Quelle freier Energie. Es gibt einen grundlegenden Kompromiss, der durch die Energieerhaltung diktiert wird.
Das Arbeits-Energie-Prinzip
In einem idealen System muss die verrichtete Arbeit am Eingangskolben gleich der Arbeit sein, die vom Ausgangskolben verrichtet wird. Arbeit wird berechnet als Arbeit = Kraft × Weg.
Der Weg-Kompromiss
Da die Ausgangskraft (F₂) viel größer ist als die Eingangskraft (F₁), muss der Weg, den der Ausgangskolben zurücklegt (D₂), proportional kleiner sein als der Weg, den der Eingangsstößel zurücklegt (D₁).
Um den massiven Arbeitskolben nur einen Zoll anzuheben, müssen Sie den kleinen Stößel möglicherweise um 100 Zoll nach unten drücken. Sie tauschen eine lange Bewegung mit geringer Kraft gegen eine kurze Bewegung mit hoher Kraft ein.
Die richtige Wahl für Ihr Ziel treffen
Das Verständnis dieses Prinzips ermöglicht es Ihnen, es auf verschiedene Ziele anzuwenden, sei es im Design, im Betrieb oder im einfachen Verständnis.
- Wenn Ihr Hauptaugenmerk auf dem Design liegt: Konzentrieren Sie sich auf das Verhältnis der Kolbenflächen (A₂/A₁), da dieses Verhältnis direkt den Kraftverstärkungsfaktor Ihres Systems bestimmt.
- Wenn Ihr Hauptaugenmerk auf dem Betrieb liegt: Erkennen Sie, dass die erzeugte Kraft zwar immens ist, die Bewegung des Arbeitskolbens jedoch langsam und bedächtig sein wird. Dieser Kompromiss zwischen Kraft und Weg ist ein zentrales Sicherheits- und Betriebsmerkmal.
- Wenn Ihr Hauptaugenmerk auf dem Verständnis liegt: Die wichtigste Erkenntnis ist, dass der Druck in einer geschlossenen Flüssigkeit konstant bleibt, wodurch eine kleine Kraft auf einer kleinen Fläche zu einer großen Kraft auf einer großen Fläche werden kann.
Durch die Beherrschung dieses Prinzips können Sie sehen, wie einfache Fluidmechanik einige der leistungsstärksten Maschinen der modernen Welt ermöglicht.
Zusammenfassungstabelle:
| Komponente | Funktion | Schlüsselprinzip |
|---|---|---|
| Stößel (Kleiner Kolben) | Übt Anfangskraft (F₁) über eine kleine Fläche (A₁) aus | Erzeugt Systemdruck (P = F₁/A₁) |
| Arbeitskolben (Großer Kolben) | Übt vervielfachte Ausgangskraft (F₂) über eine große Fläche (A₂) aus | Wandelt Druck in Kraft um (F₂ = P × A₂) |
| Inkompressible Flüssigkeit | Überträgt den Druck unvermindert durch das gesamte System | Kern des Pascalschen Gesetzes |
| Kraftverstärkung | Ausgangskraft ist Eingangskraft multipliziert mit dem Flächenverhältnis (F₂ = F₁ × (A₂/A₁)) | Erreicht durch Tausch von Weg gegen Kraft |
Benötigen Sie präzise, leistungsstarke Kraft für Ihre Laboranwendungen? KINTEK ist spezialisiert auf hochwertige Laborgeräte, einschließlich hydraulischer Pressen, die für Zuverlässigkeit und exakte Leistung ausgelegt sind. Ob Sie Proben komprimieren, Materialien formen oder eine kundenspezifische Kraftanwendung benötigen, unsere Expertise stellt sicher, dass Sie das richtige Werkzeug für Ihre Anforderungen erhalten. Kontaktieren Sie noch heute unsere Experten, um die perfekte hydraulische Pressenlösung für Ihr Labor zu finden!
Visuelle Anleitung
Ähnliche Produkte
- 600T Vakuum-Induktions-Heißpressofen zur Wärmebehandlung und Sinterung
- Vakuum-Heißpress-Ofen Beheizte Vakuum-Pressmaschine Rohröfen
- Hochdruck-Labor-Vakuumröhrentiegelofen Quarzrohr-Ofen
- Vakuumwärmebehandlungs- und Sinterofen mit 9 MPa Luftdruck
- 1400℃ Labor-Quarzrohr-Ofen mit Aluminiumoxidrohr-Röhrenofen
Andere fragen auch
- Kann man einen elektrischen Lichtbogen im Vakuum erzeugen? Wie Hochspannung Plasma in einem Vakuum erzeugt
- Wovon hängt die Haftfestigkeit beim Hartlöten ab? Meistern Sie die 3 Schlüssel zu einer starken Verbindung
- Wie funktioniert Heißpressen? Maximale Dichte für fortschrittliche Materialien erreichen
- Warum unterliegen hartgelötete Verbindungen Ermüdungsversagen? Die kritischen Faktoren für langlebige Verbindungen verstehen
- Welchen Vorteil bietet das Warmpressen? Erzielen Sie stärkere, komplexere Teile
